NOT: Bu metinde, İngilizce’de “blocked practice” ve “interleaved practice” olarak adlandırılan iki farklı öğrenme yaklaşımı ele alınmaktadır. “Blocked practice” için Türkçe’de Bloklu Alıştırma, Blok Çalışma, veya Sıralı Pratik gibi ifadeler kullanılabilir. “Interleaved practice” ise Karışık Alıştırma, Aralıklı Çalışma, ya da Karma Öğrenim şeklinde çevrilebilir. Bu terimler, farklı öğretim yöntemlerini açıklamak için kullanılacaktır.
Giriş
Kesirlerin öğrenilmesi, matematik eğitiminde temel bir dönüm noktasıdır ancak öğrenciler için genellikle zorluk teşkil eder. Bu konuda öğretim stratejileri arasında fiziksel materyallerin, dijital platformların ve *blok* (konuların sırayla işlenmesi) veya *aralıklı* (farklı konuların karıştırılarak işlenmesi) gibi yöntemlerin kullanımı yer alır. Bu makale, bu yaklaşımları analiz ederek kesirlerin öğretimindeki etkinliklerini değerlendirmektedir.
Blok ve Aralıklı Pratik
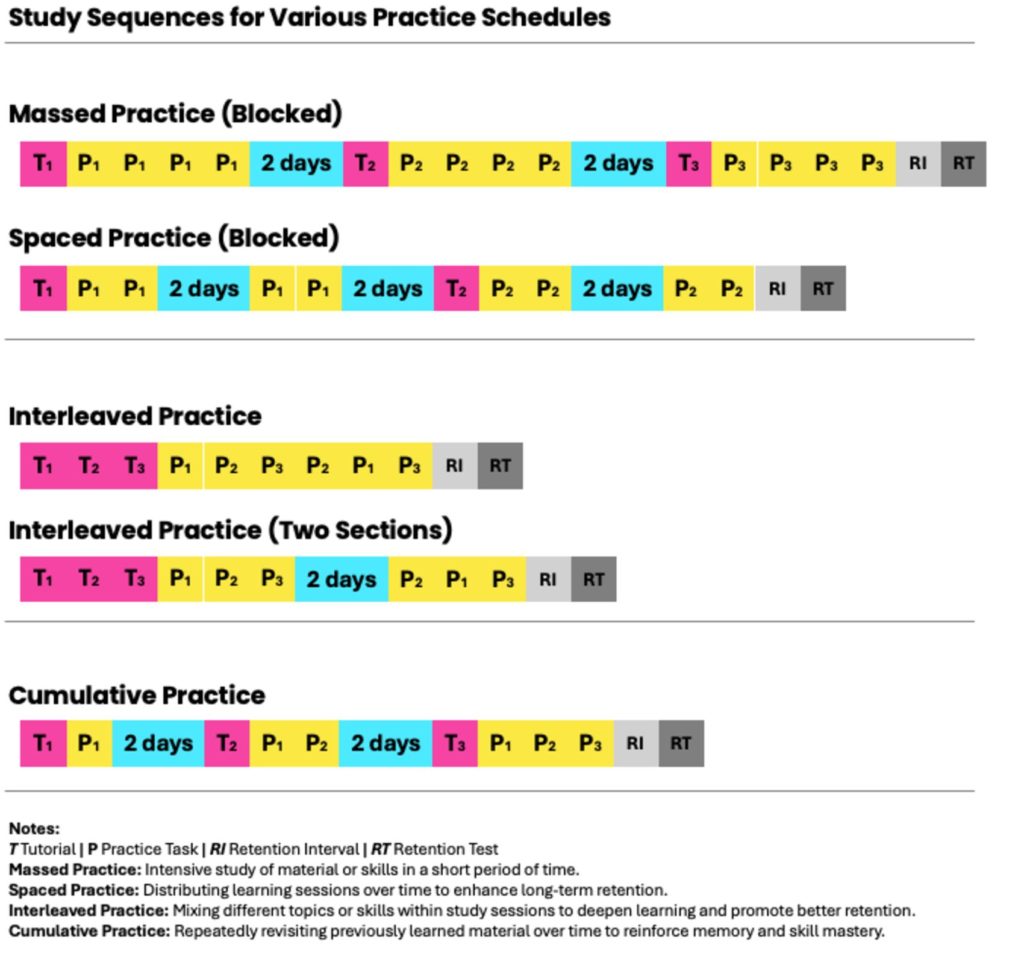
Blok pratikte bir konu tanıtıldıktan sonra, bu konuyla ilgili alıştırmalar yapılır. Bu yöntem, öğrencilerin öğrenilen kavramlara odaklanmasını sağlar. Aralıklı pratikte ise birden fazla konudan sorular karıştırılarak sunulur. Bu yaklaşım, öğrencilerin çözüm stratejilerini seçmesini gerektirir, derinlemesine öğrenmeyi ve bilginin uzun vadeli hatırlanmasını destekler. Araştırmalar, aralıklı pratiğin genel olarak öğrenme sonuçlarını iyileştirdiğini göstermiştir ancak bazı durumlarda blok pratiğin daha etkili olabileceği de belirtilmiştir.
Kesir Öğreniminde Aralıklı Pratik
Kesirler matematik eğitiminde zorlu bir konu olarak kabul edilir. Araştırmalar, aralıklı pratiğin kesirler gibi karmaşık konularda derinlemesine öğrenmeyi destekleyebileceğini göstermektedir. Ancak, ön bilgi düzeyi düşük öğrenciler için blok pratiğin başlangıçta daha faydalı olabileceği vurgulanmaktadır. Bununla birlikte, bu iki yöntemin bir arada kullanılması, hem temel bilgi edinimi hem de uzun vadeli öğrenme açısından daha etkili bir yaklaşım olabilir.
Video Tabanlı Öğrenim ve Blok Pratik
Video tabanlı öğrenim, özellikle yazılım eğitimlerinde, bilgi aktarımını standartlaştırmak için sıklıkla kullanılmaktadır. Çalışmalar, bu yöntemde blok pratiğin etkinliğini desteklemekte, aralıklı pratik ile karşılaştırıldığında önemli bir fark yaratmadığını göstermektedir.
Sonuç ve Uygulama Önerileri
Aralıklı pratik, matematik ve fizik gibi alanlarda öğrencilerin çeşitli problem türlerini çözme becerisini artırabilir. Ancak, bu yöntemin etkili olabilmesi için eğitim materyallerinin dikkatlice hazırlanması gereklidir. Blok pratik, yeni bilgilerin tanıtımı için uygun bir başlangıç yöntemidir, ancak bu bilgiler aralıklı pratikle pekiştirilebilir. Kesirlerin öğretiminde her iki yöntemin birleşik kullanımı, öğrenci ihtiyaçlarını daha iyi karşılayabilir. Daha fazla araştırma, bu yöntemlerin farklı öğrenme gruplarında nasıl uygulanabileceğini anlamamıza yardımcı olacaktır.
Kaynakça
Brunmair, M., & Richter, T. (2019). Similarity matters: A meta-analysis of interleaved learning and its moderators.. Psychological bulletin. https://doi.org/10.1037/bul0000209
Dunlosky, J., Rawson, K. A., Marsh, E. J., Nathan, M. J., & Willingham, D. T. (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public Interest, 14(1), 4-58.
Foster, N., Mueller, M., Was, C., Rawson, K., & Dunlosky, J. (2019). Why does interleaving improve math learning? The contributions of discriminative contrast and distributed practice. Memory & Cognition, 47, 1088 – 1101. https://doi.org/10.3758/s13421-019-00918-4
Fuchs, L. S., Malone, A. S., Preacher, K. J., Cho, E., Fuchs, D., & Changas, P. (2023). Next-generation fraction intervention and the long-term advantage of interleaved instruction. Exceptional Children, 89(3), 332-352.
Gabriel, F., Coché, F., Szűcs, D., Carette, V., Rey, B., & Content, A. (2013). A componential view of children’s difficulties in learning fractions. Frontiers in Psychology, 4. https://doi.org/10.3389/fpsyg.2013.00715
Getenet, S., & Callingham, R. (2017). Teaching fractions for understanding: addressing interrelated concepts. Mathematics Education Research Group of Australasia, 2017, 277-284.
Lin, C., Knowlton, B., Chiang, M., Iacoboni, M., Udompholkul, P., & Wu, A. (2011). Brain–behavior correlates of optimizing learning through interleaved practice. NeuroImage, 56, 1758-1772. https://doi.org/10.1016/j.neuroimage.2011.02.066
Lortie-Forgues, H., Tian, J., & Siegler, R. S. (2015). Why is learning fraction and decimal arithmetic so difficult? Developmental Review, 38, 201–221. https://doi.org/10.1016/j.dr.2015.07.008
Nemeth, L., Werker, K., Arend, J., & Lipowsky, F. (2021). Fostering the acquisition of subtraction strategies with interleaved practice: An intervention study with German third graders. Learning and Instruction, 71, 101354. https://doi.org/10.1016/j.learninstruc.2020.101354
Nuketayeva, K. (2021). The effect of practice schedules in video-based software training: Schedule of practice matters. Does it matter for video-based software training? (Master’s thesis, University of Twente).
Pan, S., Tajran, J., Lovelett, J., Osuna, J., & Rickard, T. (2019). Does interleaved practice enhance foreign language learning? The effects of training schedule on Spanish verb conjugation skills.. Journal of Educational Psychology. https://doi.org/10.1037/EDU0000336
Patel, R., Liu, R., & Koedinger, K. (2016). When to Block versus Interleave Practice? Evidence Against Teaching Fraction Addition before Fraction Multiplication. Cognitive Science.
Rau, M., Aleven, V., & Rummel, N. (2010). Blocked versus Interleaved Practice with Multiple Representations in an Intelligent Tutoring System for Fractions. , 413-422. https://doi.org/10.1007/978-3-642-13388-6_45
Rau, M., Aleven, V., & Rummel, N. (2013). Interleaved Practice in Multi-Dimensional Learning Tasks: Which Dimension Should We Interleave?.. Learning and Instruction, 23, 98-114. https://doi.org/10.1016/J.LEARNINSTRUC.2012.07.003
Rohrer, D., Dedrick, R. F., & Stershic, S. (2015). Interleaved practice improves mathematics learning. Journal of Educational Psychology, 107(3), 900–908. https://doi.org/10.1037/edu0000001
Rohrer, D., Dedrick, R. F., Hartwig, M. K., & Cheung, C.-N. (2020). A randomized controlled trial of interleaved mathematics practice. Journal of Educational Psychology, 112(1), 40–52. https://doi.org/10.1037/edu0000367
Sharp, J., & Adams, B. (2002). Children’s Constructions of Knowledge for Fraction Division After Solving Realistic Problems. The Journal of Educational Research, 95(6), 333–347. https://doi.org/10.1080/00220670209596608
Stambaugh, L. (2011). When Repetition Isn’t the Best Practice Strategy: Effects of Blocked and Random Practice Schedules. Journal of Research in Music Education, 58, 368 – 383. https://doi.org/10.1177/0022429410385945
Tian, J., & Siegler, R. S. (2017). Fractions Learning in Children With Mathematics Difficulties. Journal of Learning Disabilities, 50(6), 614–620. https://doi.org/10.1177/0022219416662032
Weinstein, Y., Madan, C. R., & Sumeracki, M. A. (2018). Teaching the science of learning. Cognitive research: principles and implications, 3, 1-17.
BU YAZI KAYNAK GÖSTERİLMEDEN KULLANILAMAZ.
![]()